Basic Simulator

Now that we are more familiar with the concept of RUMEs, let’s run some simulations.

BasicSimulator is the main tool for the job. It runs one forward simulation at a time and produces one simulation output which records how the model’s state evolved over the duration.

Starting with the same RUME we’ve been using…

from epymorph.kit import *
from epymorph.adrio import us_tiger

rume = SingleStrataRUME.build(
    ipm=ipm.SIRS(),
    mm=mm.Centroids(),
    init=init.SingleLocation(location=0, seed_size=100),
    scope=StateScope.in_states(["AZ", "CO", "NM", "UT"], year=2020),
    time_frame=TimeFrame.rangex("2020-01-01", "2021-01-01"),
    params={
        "beta": 0.3,
        "gamma": 1/5,
        "xi": 1/90,
        "population": [7_151_502, 5_773_714, 2_117_522, 3_271_616],
        "centroid": us_tiger.InternalPoint(),
    },
)

Running a Simulation

We can construct a simulator passing in this RUME:

sim = BasicSimulator(rume)

And use sim’s run() method to execute the simulation and produce a single simulation output, sometimes called a “realization”:

out = sim.run()

Easy as that!

Overriding Params

The run method gives us a few options worth mentioning. First, we can override some or all of the RUME parameters for the sake of a single realization with the params parameter. For instance, we could quickly explore the effects of different beta values without having to rebuild our RUME.

sim.run(
    params={
        "beta": 0.4,
    },
)

sim.run(
    params={
        "beta": 0.5,
    },
)

This params dictionary follows the same rules as the params dictionary we provided to the RUME, so we don’t lose any flexibility by specifying values this way.

Controlling Randomness

Normally each run is subject to random variations by design. But if we provide a random number generator with a specific seed, we’ll get the same results every time. The rng_factory parameter accepts a function of arity zero (no parameters) that returns a numpy.random.Generator instance.

# default_rng from the epymorph.kit import works
sim.run(rng_factory=default_rng(42))


# or we could define our own function
from numpy.random import Generator, SFC64

def my_rng():
    return Generator(SFC64(42))

sim.run(rng_factory=my_rng)


# or use Python's lambda syntax
sim.run(rng_factory=lambda: Generator(SFC64(42)))

Next we’ll briefly inspect the simulation output that BasicSimulator produces.

Simulation Output

A quick aside about the IPM

Let’s take a moment to inspect the canonical SIRS disease model before continuing, and how epymorph represents its features. This is a compartmental model, and we can diagram its compartments and the transitions between compartments like this:

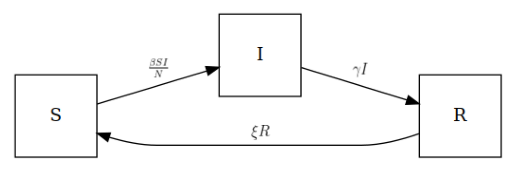
Diagram of a classical SIRS compartment model.

This model represents a disease where individuals are considered to be in one of three states (the nodes of the graph):

Susceptible: they may become infected if they come into contact with an infectious individual,
Infectious: they are currently infected and may spread the disease to others, and
Recovered: they have recovered from an infection and currently have some immunity to catching the disease again.

The arrows (the directed edges of the graph) indicate the possible transitions. When an individual does transition from one state to another, this is an event. Becoming infected, transitioning from susceptible to infectious, is the S-to-I event or \(S{\to}I\).

In epymorph the order of these compartments and events is critical. Thankfully we can inspect the ipm object to print this information if we need to.

print("compartments:", [str(c.name) for c in rume.ipm.compartments])
print("events:", [str(e.name) for e in rume.ipm.events])

compartments: ['S', 'I', 'R']
events: ['S → I', 'I → R', 'R → S']

Initial Conditions

Our out object (an instance of the Output class) contains a bunch of neat data. For instance, we can look at the initial conditions of the simulation:

out.initial

array([[7151402,     100,       0],
       [5773714,       0,       0],
       [2117522,       0,       0],
       [3271616,       0,       0]])

The API doc for Output.initial tells us this is an array of shape (N,C) – N for geo nodes and C for IPM compartments. So knowing that, we can now read this array. The first row is for the first location, Arizona, the second for Colorado, and so on. And the columns are the IPM compartments \(S\), \(I\), and \(R\). Just as we would expect, we started with 100 infected individuals in Arizona, and all other individuals are susceptible. No one starts out as recovered – which in epidemiology terms means our population is naive to this hypothetical pathogen.

Compartments

So if that’s how the simulation started, how did things go from there? Imagine that we advance our simulation by one time-step then record this same info. Here we go:

out.compartments[0, :, :]

array([[7151157,     104,       7],
       [5773533,       0,       0],
       [2117803,       0,       0],
       [3271750,       0,       0]])

There’s a few more infected folks and some recovered. Blink forward again:

out.compartments[1, :, :]

array([[7151369,     106,      27],
       [5773714,       0,       0],
       [2117522,       0,       0],
       [3271616,       0,       0]])

Even more folks become infected and some more recover. We get a sense that the simulation is evolving.

The compartments array tracks the time-series data of how many individuals are in each IPM compartment at each simulation location. It’s a (T,N,C)-shaped numpy array, and I’ve used numpy’s indexing features to look at one time-slice at a time. Since this is just a numpy array, we can inspect a few of its critical aspects:

cs = out.compartments
print(f"{type(cs)=}")
print(f"{cs.dtype=}")
print(f"{cs.shape=}")

type(cs)=<class 'numpy.ndarray'>
cs.dtype=dtype('int64')
cs.shape=(732, 4, 3)

And we can use the array to perform interesting calculations, like what was the maximum number of people infected at one time in each US State throughout the simulation? (As we saw, the \(I\) compartment is second in the IPM order, which corresponds to index 1 in Python.)

out.compartments[:, :, 1].max(axis=0)

array([510135, 408920, 150067, 231632])

Events

The compartment values (sometimes called state variables) of our simulation is only one view however. Looking at the above we can’t tell exactly how many people caught the disease during that second time step. The number of infectious individuals changed, but that is a combination of people becoming infected as well as people recovering – there’s an in-flux and out-flux from the \(I\) compartment. In this case we can’t figure it out from looking at the other compartments either, because each of those are also subject to in-flux and out-flux. If you’re just counting the number of people in a room, you get the same number regardless if five leave and five enter or if six leave and six enter.

So we also need to know exactly how many individuals transitioned between each of the compartments at every time step. epymorph records this in the events array.

out.events[1, :, :]

array([[22, 20,  0],
       [ 0,  0,  0],
       [ 0,  0,  0],
       [ 0,  0,  0]])

The events array is (T,N,E)-shaped, where E is the number of possible events in our model. So in this case, we get a row per US State and a column per event: \(S{\to}I\), \(I{\to}R\), and \(R{\to}S\). Now we have the complete picture of how the simulation state changed at every time step.

Other Utilities

Aside from the simulation results data, Output also holds onto useful metadata about the simulation that produced the output. Most importantly we can recall our RUME with out.rume and then further query the RUME as needed.

# TimeFrame objects print as ISO-8601 date ranges and duration
print(out.rume.time_frame)

2020-01-01/2020-12-31 (366D)

If we would prefer to work with our data as a Pandas DataFrame, that’s also supported. We get a table where the time and geo node axes are in “long” format, while the compartments and events are “wide”.

df = out.dataframe

print(f"{type(df)=}")

df.head() # This is a big dataframe, so just display the head of it.

type(df)=<class 'pandas.core.frame.DataFrame'>

	tick	date	node	S	I	R	S → I	I → R
0	0	2020-01-01	04	7151157	104	7	11	7
1	0	2020-01-01	08	5773533	0	0	0	0
2	0	2020-01-01	35	2117803	0	0	0	0
3	0	2020-01-01	49	3271750	0	0	0	0
4	1	2020-01-01	04	7151369	106	27	22	20

And out.ticks_in_days produces an array that converts the simulation time ticks into their equivalent in fractional days. In this simulation, the first simulation step covers one-third of a day while the next covers the remaining two-thirds of a day, and so on repeatedly.

import numpy as np

# using np.printoptions() just for nicer formatting...
with np.printoptions(precision=3, floatmode="fixed"):
    print(out.ticks_in_days[0:8])

[0.333 1.000 1.333 2.000 2.333 3.000 3.333 4.000]