Estimating time-varying transmission rate from data

SCENARIO:

A particle filter is an algorithm which can use data to estimate a parameter, such as the transmission rate. The particle filter accomplishes this by combining the data with a mathematical model.

This vignette will demonstrate how to use epymorph’s built-in particle filter to estimate a time-varying transmission rate (beta) using weekly influenza hospitalization data. In the first exercise, we will define our model setup and generate synthetic data (fake data used for testing) which will be used to validate the particle filter. In the second exercise, we will setup the particle filter and run it on the synthetic data we generated in the first exercise. By validating the particle filter setup on synthetic data first, we can diagnose any issues before moving on to real data. In the third exercise, we will run the particle filter on real influenza hospitalization data. Because we will have already tested the particle filter on synthetic data, this step will be as easy as swapping out the synthetic data for the real data.

Exercise 1

In this first exercise, we will setup out mathematical model and generate synthetic data.

from epymorph.adrio import acs5, csv
from epymorph.data.ipm.sirh import SIRH
from epymorph.data.mm.no import No
from epymorph.initializer import Proportional
import numpy as np

from epymorph.kit import *

• Generate a time series for beta, which will be used to generate the synthetic data. In this case, we’ll assume a sinusoidal function to force beta.

num_weeks = 26
duration = 7 * num_weeks + 1
t = np.arange(0, duration)
true_beta = 0.05 * np.cos(t * 2 * np.pi / (365)) + 0.25

• Plot the values of this “true” or known transmission rate over time.

import matplotlib.pyplot as plt

plt.plot(t, true_beta)
plt.ylabel("beta")
plt.xlabel("time (days)")
plt.title("The transmission rate (beta) over time")
plt.show()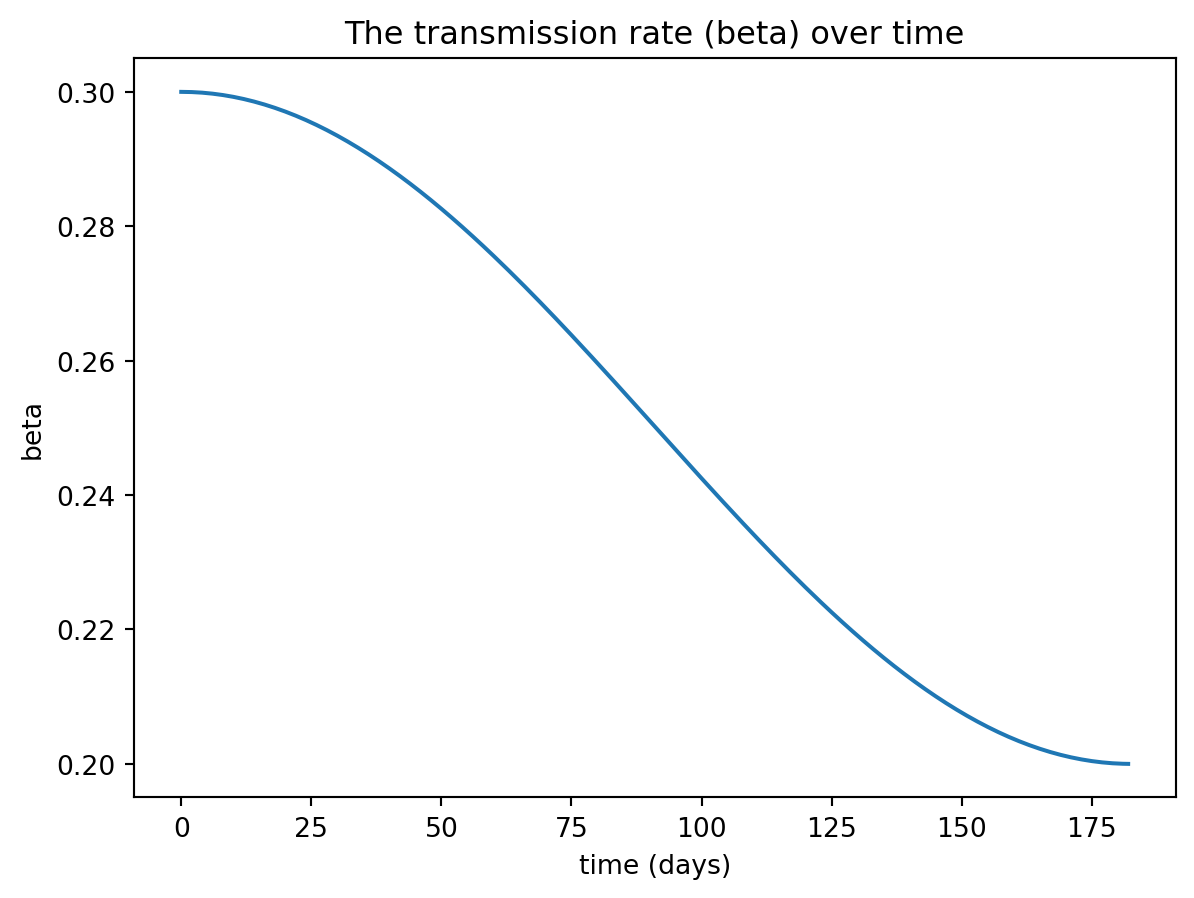

• Setup the model that will be used in the particle filter. It is important that the model has a hospitalized compartment since the real data is hospitalization data. In this case, we’ll use epymorph’s biult in SIRH model. Visualize the model diagram to confirm our understanding. We can see there is a fork between the I -> H and the I->R

my_ipm = SIRH()
my_ipm.diagram()

• Generate a RUME using an Arizona State-level scope, and other requirements as specified below.

rume = SingleStrataRUME.build(
    ipm=SIRH(),
    mm=No(),
    scope=StateScope.in_states(["AZ"], year=2015),
    init=Proportional(ratios=np.array([9999, 1, 0, 0], dtype=np.int64)),
    time_frame=TimeFrame.of("2022-09-15", 7 * 26 + 1),
    params={
        "beta": true_beta,
        "gamma": 0.2,
        "xi": 1 / 365,
        "hospitalization_prob": 200 / 100_000,
        "hospitalization_duration": 5.0,
        "population": acs5.Population(),
    },
)

• Run the model.

rng = np.random.default_rng(seed=1)

sim = BasicSimulator(rume)
with sim_messaging(live = False):
    out = sim.run(rng_factory=(lambda: rng))

Loading gpm:all::init::population (epymorph.adrio.acs5.Population):
  |####################| 100%  (1.010s)
Running simulation (BasicSimulator):
• 2022-09-15 to 2023-03-16 (183 days)
• 1 geo nodes
  |####################| 100% 
Runtime: 0.053s

• Use epymorph’s aggregation functionality to aggregate the weekly hospitalizations, then save the synthetic data to a .csv file. In this case we are specifying that the data observations are new hospitalizations, aggregated per seven days.

from epymorph.time import EveryNDays
from epymorph.tools.data import munge

quantity_selection = rume.ipm.select.events("I->H")
time_selection = rume.time_frame.select.all().group(EveryNDays(7)).agg()
geo_selection = rume.scope.select.all()

cases_df = munge(
    out,
    quantity=quantity_selection,
    time=time_selection,
    geo=geo_selection,
)

cases_df.to_csv("temp_synthetic_data.csv", index=False)

Exercise 2

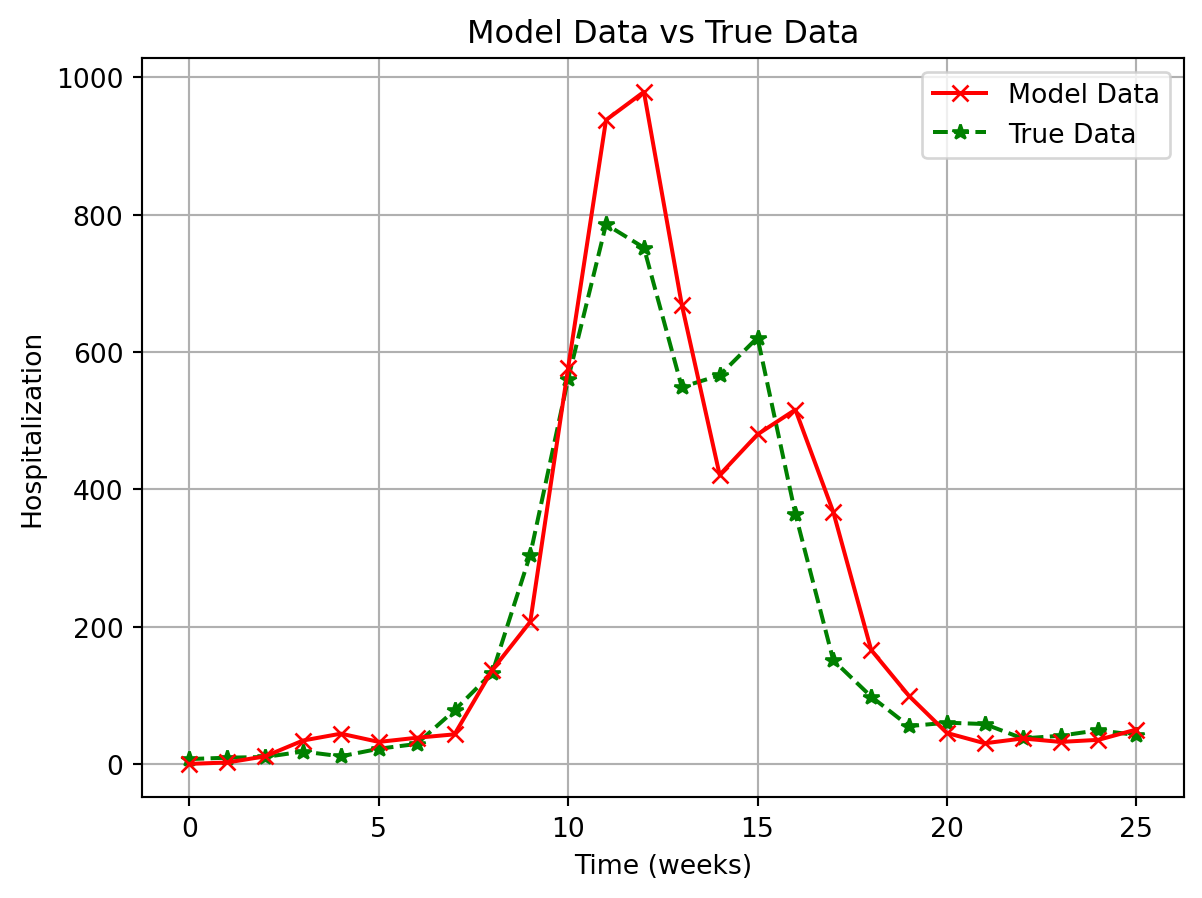
In this second exercise, we will run the particle filter on the synthetic data we generated and compare the estimate of beta produced by the particle filter to the true values of beta which were used to generate the data.

• Load the synthetic data from the .csv file. In this case, we are leveraging epymorph’s CSV ADRIO functionality.

from pathlib import Path

csvadrio = csv.CSVTimeSeries(
    file_path=Path("temp_synthetic_data.csv"),
    time_col=0,
    time_frame=rume.time_frame,
    key_col=1,
    data_col=2,
    data_type=int,
    key_type="geoid",
    skiprows=1,
)

• Create the model link, which defines how the model and data are linked, using the same selectors used to generate the data.

from epymorph.parameter_fitting.utils.observations import ModelLink

model_link=ModelLink(
    quantity=quantity_selection,
    time=time_selection,
    geo=geo_selection,
)

• Create the observations object and use the Poisson likelihood as the likelihood function used to evaluate the model predictions.

from epymorph.parameter_fitting.likelihood import Poisson
from epymorph.parameter_fitting.utils.observations import Observations

observations = Observations(
    source=csvadrio,
    model_link=model_link,
    likelihood=Poisson(),
)

• There are many types of filtering algorithms. Use a particle filter for the filter type.

from epymorph.parameter_fitting.filter.particle_filter import ParticleFilter

filter_type = ParticleFilter(num_particles=200)

• Specify which parameter(s) are to be estimated. Specify beta as a time-varying parameter with uniform initial distribution and geometric Brownian motion (GBM) for its dynamics. GBM is useful since it ensures beta will always be positive.

from epymorph.parameter_fitting.distribution import Uniform
from epymorph.parameter_fitting.dynamics import GeometricBrownianMotion
from epymorph.parameter_fitting.utils.parameter_estimation import EstimateParameters

params_space = {
    "beta": EstimateParameters.TimeVarying(
        distribution=Uniform(a=0.05, b=0.5),
        dynamics=GeometricBrownianMotion(volatility=0.05),
    ),
}

• Create the filter simulation object using the RUME, observations, filter type, and parameter space we defined above.

from epymorph.parameter_fitting.particlefilter_simulation import FilterSimulation

sim = FilterSimulation(
    rume=rume,
    observations=observations,
    filter_type=filter_type,
    params_space=params_space,
)

• Plot the observation data from this FilterSimulation object.

plt.bar(range(len(sim.cases)), sim.cases[:, 0])
plt.title("Observations")
plt.xlabel("Time (weeks)")
plt.ylabel("Hospitalizations")
plt.grid(True)
plt.show()

• Run the particle filter simulation.

output = sim.run(rng=rng)

• Plot the estimated values of beta compared to the true values.

key = "beta"

key_quantiles = np.array(output.param_quantiles[key])

plt.fill_between(
    np.arange(0, len(key_quantiles)),
    key_quantiles[:, 3, 0],
    key_quantiles[:, 22 - 3, 0],
    facecolor="blue",
    alpha=0.2,
    label="Quantile Range (10th to 90th)",
)
plt.fill_between(
    np.arange(0, len(key_quantiles)),
    key_quantiles[:, 6, 0],
    key_quantiles[:, 22 - 6, 0],
    facecolor="blue",
    alpha=0.4,
    label="Quantile Range (25th to 75th)",
)

plt.plot(
    np.arange(0, len(key_quantiles)),
    key_quantiles[:, 11, 0],
    color="red",
    label="Median (50th Percentile)",
)

obs = np.arange(0, len(key_quantiles))
plt.plot(
    1/7*t,
    true_beta,
    "k--",
    label="Truth"
)

plt.title(f"Estimate of '{key}'")
plt.xlabel("Time (weeks)")
plt.ylabel("Quantiles")
plt.legend(loc="upper right")
plt.grid(True)
plt.show()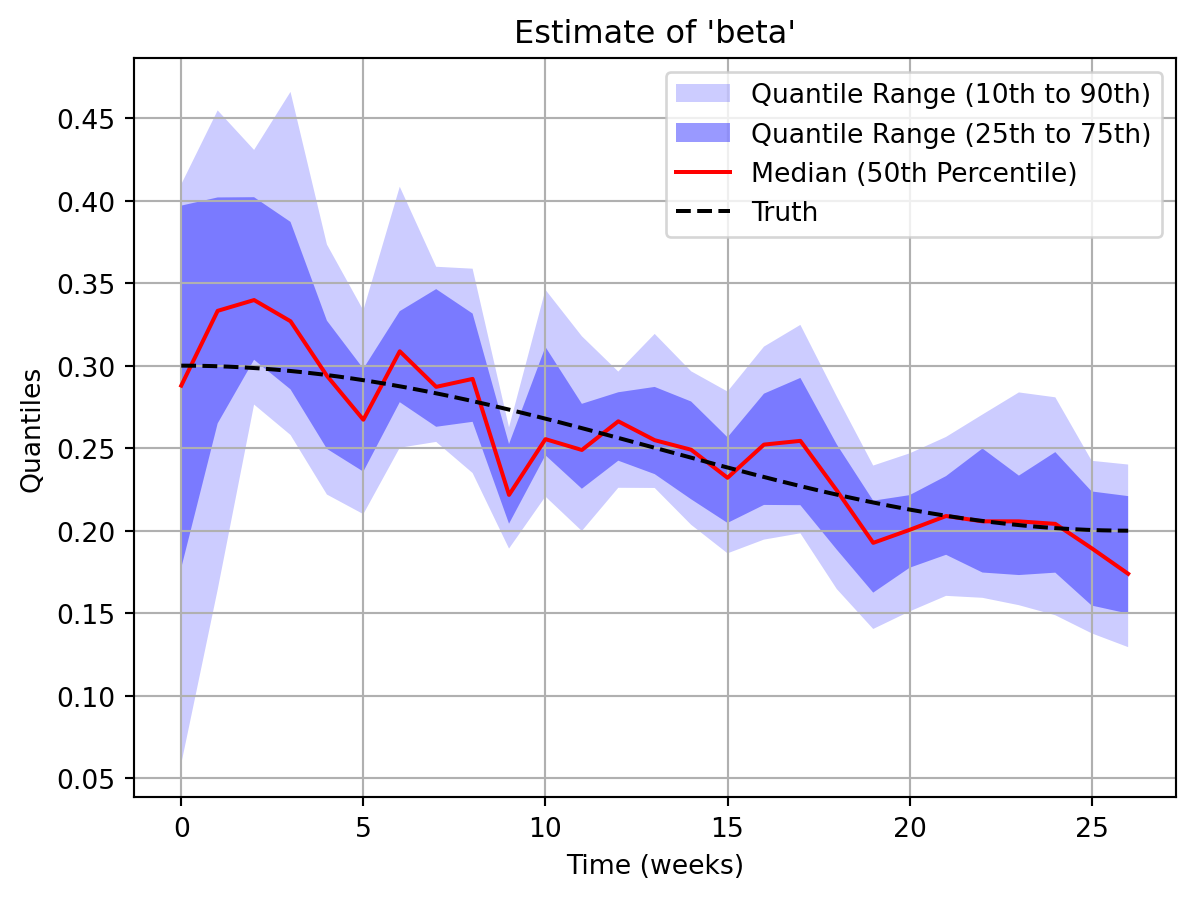

• Compare the hospitalizations expected by the model to the actual number of hospitalizations.

plt.plot(
    output.model_data[:, 0],
    label="Model Data",
    color="red",
    linestyle="-",
    zorder=10,
    marker="x",
)

plt.plot(
    output.true_data[:, 0],
    label="True Data",
    color="green",
    linestyle="--",
    zorder=9,
    marker="*",
)

plt.xlabel("Time (weeks)")
plt.ylabel("Hospitalization")
plt.title("Model Data vs True Data")
plt.legend(loc="upper right")
plt.grid(True)

plt.show()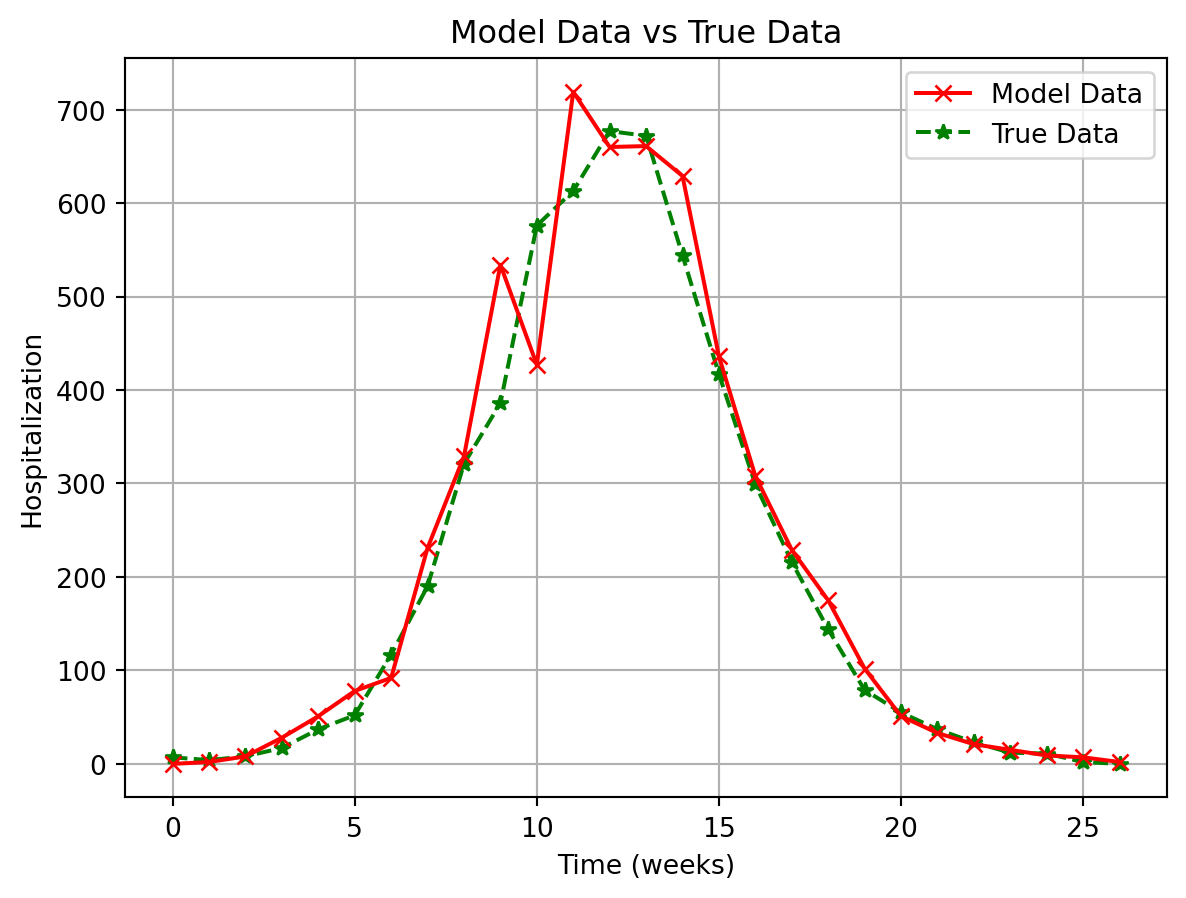

Exercise 3

In this third exercise, we apply the particle filter to real hospitalization data in order to estimate beta. This shows how we can automatically draw data from public sources, in this case the CDC, and link those data to the RUME within epymorph. Because we already tested the setup on synthetic data, we can reuse many of the same objects we defined in the second exercise.

• Modify the observations object by changing the source of the data to the CDC ADRIO.

from epymorph.adrio.cdc import InfluenzaHospitalizationSumState

observations = Observations(
    source=InfluenzaHospitalizationSumState(),
    model_link=model_link,
    likelihood=Poisson(),
)

• Create the filter simulation using the new observations object. Here is where epymorph works behind the scenes to grab the CDC data and conform it to the correct temporal and spatial aggregation specified in the RUME and the Model Link objects.

sim = FilterSimulation(
    rume=rume,
    observations=observations,
    filter_type=filter_type,
    params_space=params_space,
)

• Plot the real data from the ADRIO.

plt.bar(range(len(sim.cases)), sim.cases[:, 0])
plt.title("Arizona Observations from CDC")
plt.xlabel("Time (weeks)")
plt.ylabel("Hospitalizations")
plt.grid(True)
plt.show()

• Run the particle filter on the real data.

output = sim.run(rng=rng)

• Plot the estimated value of beta over time. Note there is no “true” value to compare to, because we are estimating from real, noisy data.

key = "beta"
node_index = 0
truth = None

key_quantiles = np.array(output.param_quantiles[key])

plt.fill_between(
    np.arange(0, len(key_quantiles)),
    key_quantiles[:, 3, 0],
    key_quantiles[:, 22 - 3, 0],
    facecolor="blue",
    alpha=0.2,
    label="Quantile Range (10th to 90th)",
)
plt.fill_between(
    np.arange(0, len(key_quantiles)),
    key_quantiles[:, 6, 0],
    key_quantiles[:, 22 - 6, 0],
    facecolor="blue",
    alpha=0.4,
    label="Quantile Range (25th to 75th)",
)

plt.plot(
    np.arange(0, len(key_quantiles)),
    key_quantiles[:, 11, 0],
    color="red",
    label="Median (50th Percentile)",
)

plt.title(f"Estimate of '{key}'")
plt.xlabel("Time (weeks)")
plt.ylabel("Quantiles")
plt.legend(loc="upper right")
plt.grid(True)
plt.show()

• Compare the expected observations to the true observations.

plt.plot(
    output.model_data[:, 0],
    label="Model Data",
    color="red",
    linestyle="-",
    zorder=10,
    marker="x",
)

plt.plot(
    output.true_data[:, 0],
    label="True Data",
    color="green",
    linestyle="--",
    zorder=9,
    marker="*",
)

plt.xlabel("Time (weeks)")
plt.ylabel("Hospitalization")
plt.title("Model Data vs True Data")
plt.legend(loc="upper right")
plt.grid(True)

plt.show()