Hospitalization IPM

SCENARIO:

In many human disease outbreaks, hospitals and hospitalization policies can have an enormous impact on overall outcomes, e.g., hospitalized persons may die at a lower rate, and may infect fewer others due to being isolated from the susceptible population. In addition, modeling hospitalization is vital for predicting evolving load on local hospital capacity, including the threat of exceeding that capacity.

The exercises in this vignette will show you how to add a basic hospitalization compartment to your model, and use it to explore some of the above hospitalization-related dynamics.

Exercise 1

• Adding hospitalization: Copy the basic SIR IPM class and edit it to add a hospitalization (‘H’) compartment to the model. Then add connections (edges) from I->H, with the rate equation “h_rate * I”. This represents the time it takes to go from infectious to hospitalized. Also add an edge from ‘H’ to ‘R’ driven by a static rate of “h_recovery * H”. For now, delete the “I” to “R” edge. This version of the model therefore assumes that all infected individuals will need to go to the hospital before recovering. Later, we will relax this unrealistic assumption. This model also assumes that hospitalized individuals do not contribute to infection dynamics. Simulate your model to observe the dynamics of each state variable.

import matplotlib.pyplot as plt
from datetime import date
from functools import partial
import numpy as np
from sympy import Max

from epymorph.kit import *
from epymorph.adrio import acs5

class initSIRH_ipm(CompartmentModel):
    compartments = [
        compartment('S'),
        compartment('I'),
        compartment('R'),
        compartment('H'),
    ]
    requirements = [
        AttributeDef('beta', type=float, shape=Shapes.TxN,
                     comment='infectivity'),
        AttributeDef('h_rate', type=float, shape=Shapes.TxN,
                     comment='progression from infected to hospitalized'),
        AttributeDef('h_recovery', type=float, shape=Shapes.TxN,
                     comment='progression from hospitalized to recovered'),
    ]

    def edges(self, symbols):
        [S, I, R, H] = symbols.all_compartments
        [β, h_rate, h_rec] = symbols.all_requirements

        N = Max(1, S + I + R + H)

        return [
            edge(S, I, rate=β * S * I / N),
            edge(I, H, rate=h_rate * I),
            edge(H, R, rate=h_rec * H),
        ]

sirh_ipm = initSIRH_ipm()
sirh_ipm.diagram()

• Initiate the requirements of the RUME.

# Use Coconino County, AZ
scope = CountyScope.in_counties(['Coconino, AZ'], year=2020)
my_init = init.SingleLocation(location=0, seed_size=10)
null_mm = mm.No()

• [] Create a RUME and run the simulation.

rume = SingleStrataRUME.build(
    ipm=initSIRH_ipm(),
    mm=null_mm,
    init=my_init,
    scope=scope,
    time_frame=TimeFrame.of("2020-01-01", 200),
    params={
        'beta': 0.4,  
        'h_rate': 1 / 10,
        'h_recovery': 1 / 50,
        'population': acs5.Population(),
    }
)

sim = BasicSimulator(rume)
with sim_messaging(live = False):
    out = sim.run(
        rng_factory=default_rng(5),
    )

Loading gpm:all::init::population (epymorph.adrio.acs5.Population):
  |####################| 100%  (1.001s)
Running simulation (BasicSimulator):
• 2020-01-01 to 2020-07-18 (200 days)
• 1 geo nodes
  |####################| 100% 
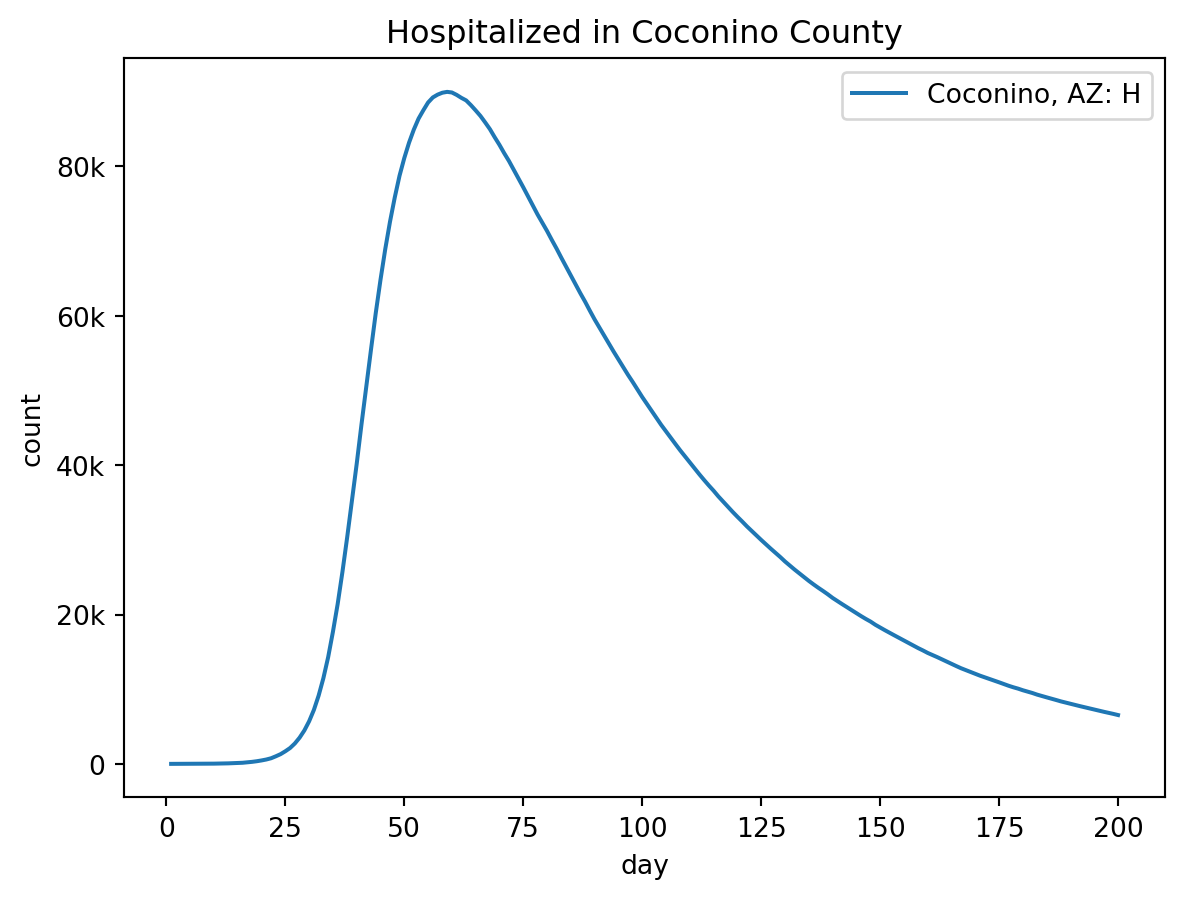
Runtime: 0.048s

• Plot the total number of Hospitalized individuals over time.

out.plot.line(
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.compartments("H"),
    title="Hospitalized in Coconino County",
)

• Plot the new hospitalization events and the new recovery events per day over time.

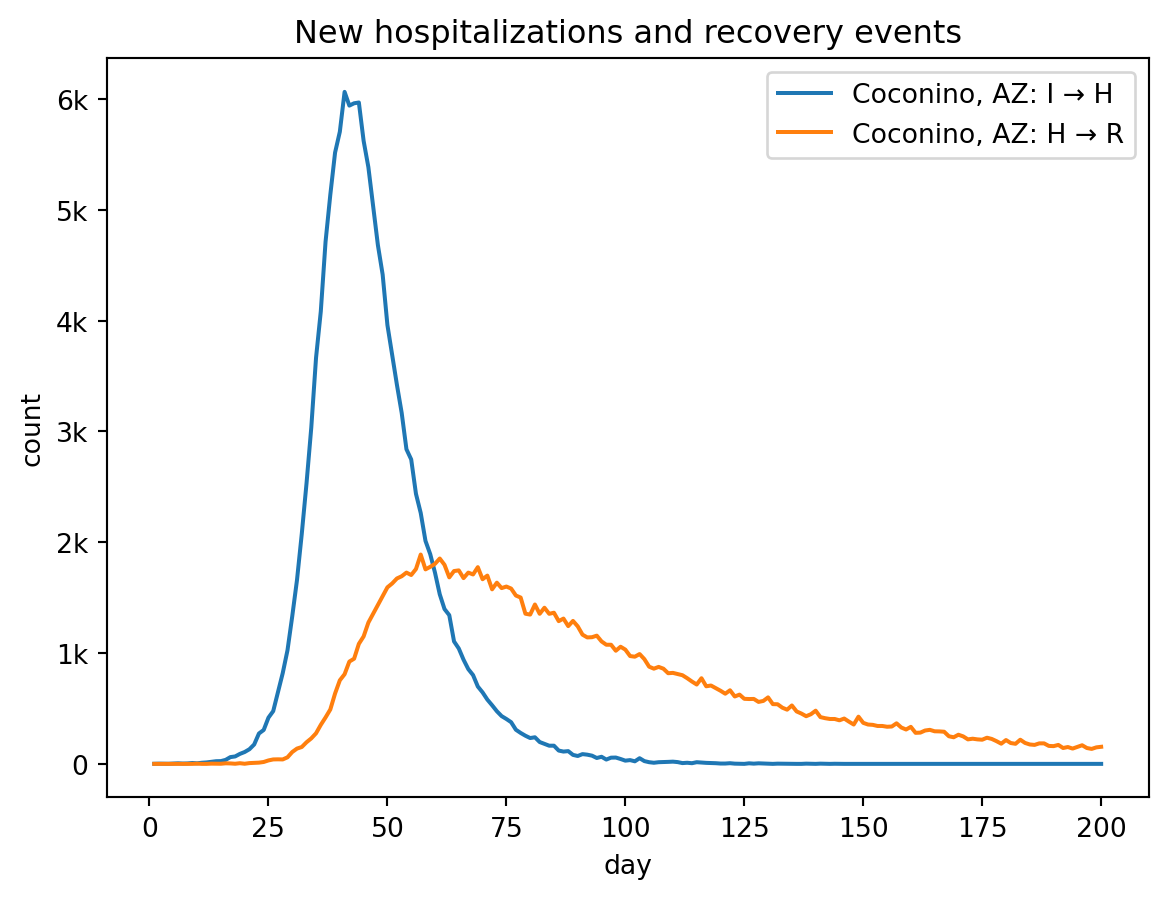
out.plot.line(
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.events("I->H", "H->R"),
    title="New hospitalizations and recovery events",
)

Exercise 2

• Adding a ‘fork’: Edit your new IPM to assume that Infectious individuals can either go to the hospital or they can recover directly. This assumption is more realistic and requires epymorph’s fork feature. You’ll also need to assign a new parameter, ‘h_prob’, that describes the probability that an individual goes to the hospital, whereas teh remaining ‘1-h_prob’ go to the recovered class. Your model should still have an edge from hospital to recovered.

# create hospitalization ipm with fork
class SIRH_ipm(CompartmentModel):
    compartments = [
        compartment('S'),
        compartment('I'),
        compartment('R'),
        compartment('H'),
    ]
    requirements = [
        AttributeDef('beta', type=float, shape=Shapes.TxN,
                     comment='infectivity'),
        AttributeDef('h_rate', type=float, shape=Shapes.TxN,
                     comment='progression from infected to hospitalized or recovered'),
        AttributeDef('h_recovery', type=float, shape=Shapes.TxN,
                     comment='progression from hospitalized to recovered'),
        AttributeDef('h_prob', type=float, shape=Shapes.TxN,
                     comment='probablity for hospital versus recovered'),
    ]

    def edges(self, symbols):
        [S, I, R, H] = symbols.all_compartments
        [β, h_rate, h_rec, h_prob] = symbols.all_requirements

        N = Max(1, S + I + R + H)

        return [
            edge(S, I, rate=β * S * I / N),
            fork(
                edge(I, H, rate=h_rate * I * h_prob),
                edge(I, R, rate=h_rate * I * (1 - h_prob)),
            ),
            edge(H, R, rate=h_rec * H)
        ]

sirh_ipm2 = SIRH_ipm()
sirh_ipm2.diagram()

• Re-run your model to observe the dynamics of each state variable.

rume = SingleStrataRUME.build(
    ipm=SIRH_ipm(),
    mm=null_mm,
    init=my_init,
    scope=scope,
    time_frame=TimeFrame.of("2020-01-01", 200),
    params={
        'beta': 0.4,  
        'h_rate': 1 / 10,
        'h_recovery': 1 / 50,
        'h_prob': 0.10,
        'population': acs5.Population(),
    }
)

sim = BasicSimulator(rume)
with sim_messaging(live = False):
    out = sim.run(
        rng_factory=default_rng(5),
    )

Loading gpm:all::init::population (epymorph.adrio.acs5.Population):
  |####################| 100%  (0.473s)
Running simulation (BasicSimulator):
• 2020-01-01 to 2020-07-18 (200 days)
• 1 geo nodes
  |####################| 100% 
Runtime: 0.044s

• Visualize the I->R and the I->H events over time. You’ll see that the number of new hospitalizations per day is much lower.

out.plot.line(
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.events("I->H", "I->R"),
    title="New hospitalizations and recovery events",
)

• Change the hospitalization probability (h_prob) to investigate the effects of a more or less dangerous pathogen and visually compare the resulting dynamics.

stored_sim_results = []
probs = [.01, .05, .10, .20]

for p in probs:
    rume = SingleStrataRUME.build(
        ipm=SIRH_ipm(),
        mm=null_mm,
        init=my_init,
        scope=scope,
        time_frame=TimeFrame.of("2020-01-01", 200),
        params={
            'beta': 0.4,
            'h_rate': 1 / 10,
            'h_recovery': 1 / 50,
            'h_prob': p,
            'population': acs5.Population(),
        }
    )

    sim = BasicSimulator(rume)
    out = sim.run(
        rng_factory=default_rng(8),
    )
    stored_sim_results.append(out)

fig, ax = plt.subplots()

for j in stored_sim_results:
    j.plot.line_plt(
        ax = ax,
        geo=j.rume.scope.select.all(),
        time=j.rume.time_frame.select.all(),
        quantity=j.rume.ipm.select.events("I->H"),
    )

ax.set_xlabel("day")
ax.set_ylabel("I to H events")
ax.set_title("Varying the probability of hospitalization")
ax.grid(False)

fig.tight_layout()
plt.show()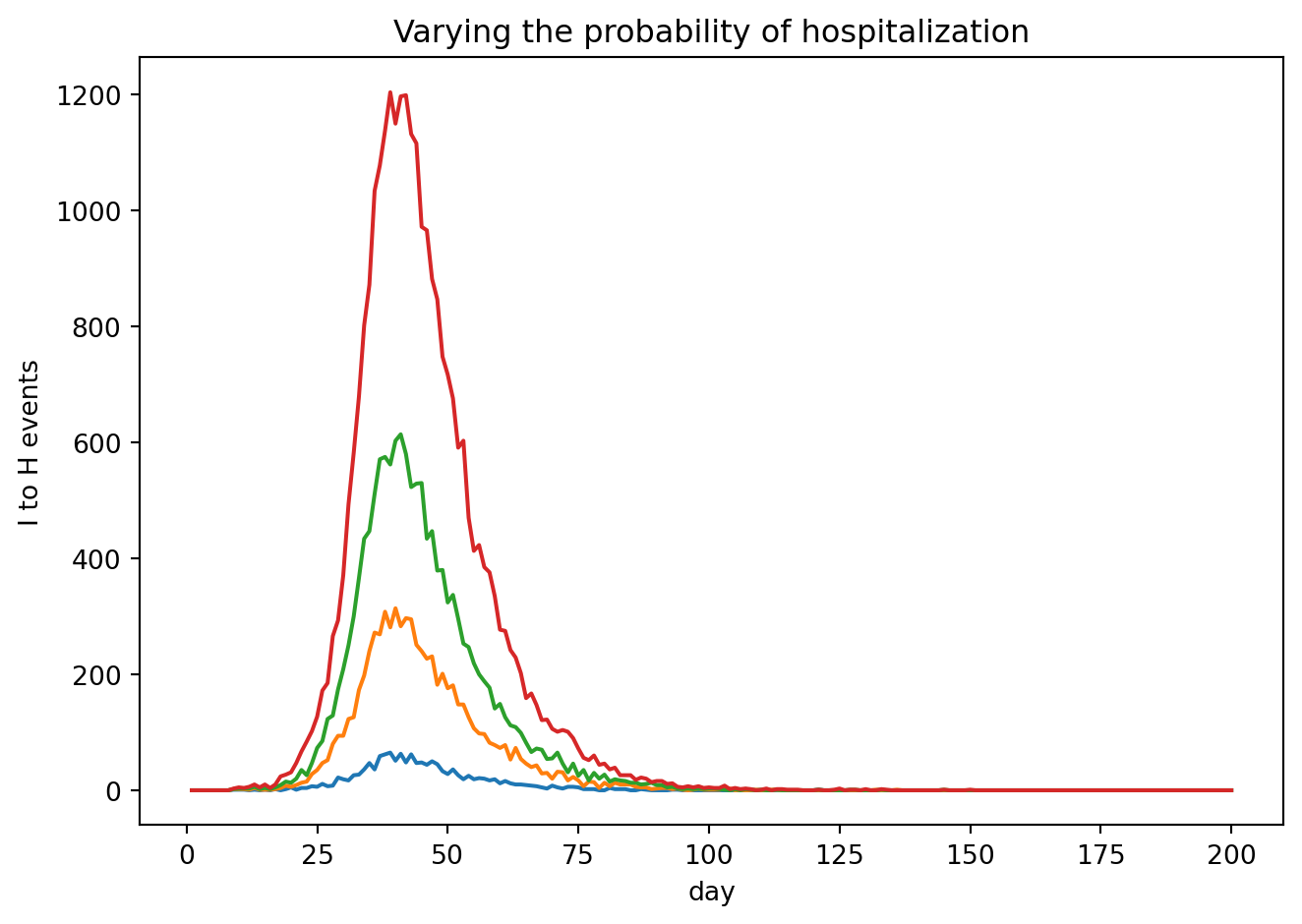

Exercise 4

• ADVANCED: Explore hospital capacity limits. All hospitals have certain capacities (total beds, ICU beds, etc) that set an upper limit on how many patients they can care for at any one time. A major concern in outbreaks is that these capacities will be reached, leading to a major health crisis as sick people are not able to be hospitalized. We can use the model we have built to explore this threat in more detail. Suppose the local hospital has a capacity of HH beds. Does your current simulation ever show this maximum capacity met or exceeded? If not, try increasing the transmission rate for this pathogen. On what day of the simulation does hospital capacity get exceeded? Can you see how decreasing beta slows the spread of infection and therefore the hospitalization curve, perhaps to the point where it never exceeds the hospital capacity limit before the infection wave peaks? This “flattening of the curve” is a main point of public health interventions (e.g. social distancing, masking, etc.), all of which can be effective in reducing transmission rate.

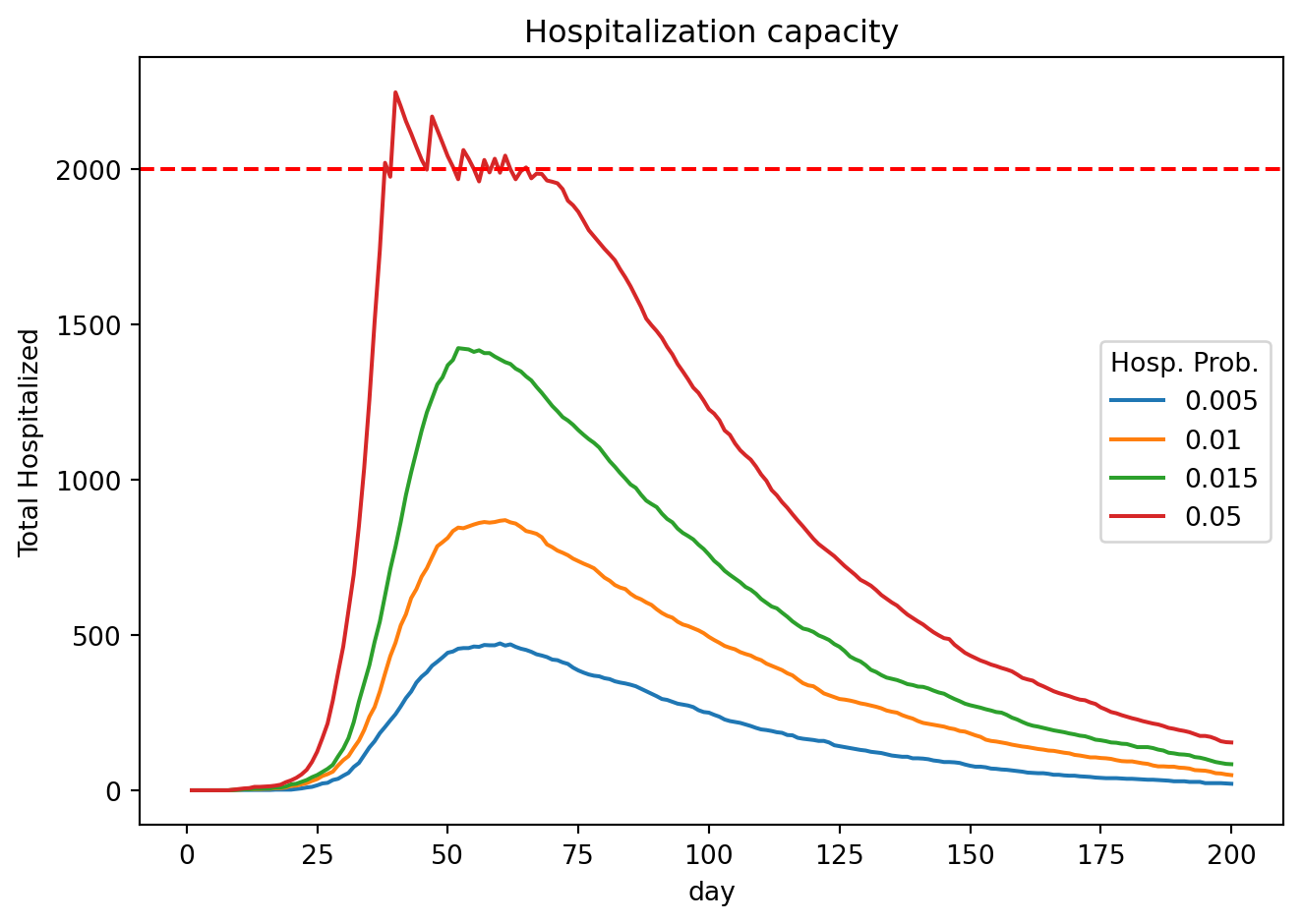
Making the limits real. What would happen if the hospital bed capacity were actually reached? In simplest terms, the ‘H’ compartment would be full, and should not be allowed to grow anymore. Let’s explore how this could be modeled in epymorph. Change the static hospitalization rate (h_rate) on the I→H edge to be represented by a stepwise function, described by the following pseudo-code: “If H< capacity h_rate=value1, else h-rate=0”, to cut off flow to the ‘H’ compartment anytime the hospital is reaching capacity. Now run your simulation again, to see if the ‘H’ compartment ever exceeds its capacity.

from sympy import Piecewise

# custom ipm to use simpy to stop at the max bed capacity (stepwise or traditional function)
class SIRH_new(CompartmentModel):
    compartments = [
        compartment('S'),
        compartment('I'),
        compartment('R'),
        compartment('H'),
    ]

    requirements = [
        AttributeDef('beta', type=float, shape=Shapes.TxN,
                     comment='infectivity'),
        AttributeDef('h_rate', type=float, shape=Shapes.TxN,
                     comment='progression from infected to hospitalized or recovered'),
        AttributeDef('h_recovery', type=float, shape=Shapes.TxN,
                     comment='progression from hospitalized to recovered'),
        AttributeDef('h_prob', type=float, shape=Shapes.TxN,
                     comment='probablity for hospital versus recovered'),
        AttributeDef('capacity', type=float, shape=Shapes.TxN,
                     comment='allowed capacity of hospital beds'),
    ]

    def edges(self, symbols):
        [S, I, R, H] = symbols.all_compartments
        [β, y, h_rec, h_prob, capacity] = symbols.all_requirements

        N = Max(1, S + I + R + H)

        return [
            edge(S, I, rate=β * S * I / N),
            fork(
                edge(I, H, rate=Piecewise((y * I * h_prob, H < capacity), (0, True))),
                edge(I, R, rate=y * I * (1 - h_prob)),
            ),
            edge(H, R, rate=h_rec * H),
        ]

# store hospitalization ipm

# hospital bed capacity (hypothetical)
capacity = 2000.0

stored_sim_results = []
probs = [.005, .01, .015, .05]

for p in probs:
    rume = SingleStrataRUME.build(
        ipm=SIRH_new(),
        mm=null_mm,
        init=my_init,
        scope=scope,
        time_frame=TimeFrame.of("2020-01-01", 200),
        params={
            'beta': 0.4,
            'h_rate': 1 / 10,
            'h_recovery': 1 / 50,
            'h_prob': p,
            'capacity': capacity,
            'population': acs5.Population(),
        }
    )

    sim = BasicSimulator(rume)
    out = sim.run(
        rng_factory=default_rng(8),
    )
    stored_sim_results.append(out)

• Modify the graphing functions at the end of your simulation to add a horizontal line to the graph, representing the limit on hospital beds, to make it more clear when the hospitalization curve hits this limit.

fig, ax = plt.subplots()

for j in stored_sim_results:
    j.plot.line_plt(
        ax = ax,
        geo=j.rume.scope.select.all(),
        time=j.rume.time_frame.select.all(),
        quantity=j.rume.ipm.select.compartments("H"),
    )

ax.set_xlabel("day")
ax.set_ylabel("Total Hospitalized")
ax.set_title("Hospitalization capacity")
ax.grid(False)

plt.legend(probs, title="Hosp. Prob.")
plt.axhline(y=capacity, color='red', linestyle='--')

fig.tight_layout()
plt.show()