Introductory usage of epymorph

SCENARIO:

Welcome to epymorph! Let’s jump into the basics of using epymorph by building a simple model for a basic scenario.

Imagine that you are investigating the dynamics of measles transmission in the children of a single US County. For simplicity, we’ll assume that the population of children within the county is mixed homogenously and all children are susceptible (i.e., a naive population). Suppose we are investigating Mohave County in Arizona.

Exercise 1

Build a simple Susceptible-Infectious-Recovered (SIR) model for a single population. Once you recover from measles, you are typically immune for life. Thus, a simple SIR model provides a suitable basis for modeling this case study.

• Begin by setting up a new modeling experiment in epymorph, within your Jupyter notebook. This involves making sure your environment is set up correctly.

# import the necessary libraries
import matplotlib.pyplot as plt
import numpy as np
from sympy import Max

from epymorph.kit import *
from epymorph.adrio import acs5

• Then use the convenient base model library of epymorph to import a basic SIR intrapopulation model (IPM) into your experiment.

class Sir(CompartmentModel):
    """Defines a compartmental IPM for a generic SIR model."""
    compartments = [
        compartment('S'),
        compartment('I'),
        compartment('R'),
    ]

    requirements = [
        AttributeDef('beta', type=float, shape=Shapes.TxN,
                     comment='infectivity'),
        AttributeDef('gamma', type=float, shape=Shapes.TxN,
                     comment='recovery rate'),
    ]

    def edges(self, symbols):
        [S, I, R] = symbols.all_compartments
        [β, γ] = symbols.all_requirements

        N = Max(1, S + I + R)

        return [
            edge(S, I, rate=β * S * I / N),
            edge(I, R, rate=γ * I),
        ]

my_ipm = Sir()

• In this example, we have a single population (i.e., node), which is the child population of Mohave County in Arizona. Use the scoping feature to specify Mohave County as the scope.

scope = CountyScope.in_counties(["Mohave, AZ"], year=2020)

• Because we have one node, we will not have any between-node movement. Thus, select the ‘null’ movement model.

null_mm = mm.No()

• You’ll need to specify an ‘initializer’ which tells epymorph how many individuals are in each state variable at the start of the simulation. Initialize with 5 infected individuals.

my_init = init.SingleLocation(location=0, seed_size=5)

• Now specify a time range for your simulation. For this example use the following time range of 200 days.

time = TimeFrame.of("2020-01-01", duration_days=200)

Now we can set up the RUME for this exercise. - To do this, you will need to specify the ‘population’ that is required by the IPM. Use the CensusAdrio to specify populations in the age range of children (0 - 9 years old) - Use the following values for the required parameters. - beta = 0.4 - gamma = 1/4

minage = 0
maxage = 9
pop = acs5.PopulationByAge(minage, maxage)
age = acs5.PopulationByAgeTable()

• Now you’ll need to assign some control parameters for the simulation, including the parameters of your IPM, how you want to initialize the infection, the county being simulated, and a time limit.

beta = 0.4
gam = 1 / 4

• Run the simulation

# create the simulation
rume = SingleStrataRUME.build(
    scope=scope,
    ipm=my_ipm,
    mm=null_mm,
    init=my_init,
    time_frame=time,
    params={
        "beta": beta,
        "gamma": gam,
        "population": pop,
        "population_by_age_table": age,
    },
)

sim = BasicSimulator(rume)
# here you may add the live = False to make the results look cleaner
with sim_messaging(live= False):
    out = sim.run(
        rng_factory=default_rng(5),
    )

Loading gpm:all::init::population_by_age_table (epymorph.adrio.acs5.PopulationByAgeTable):
  |####################| 100%  (19.009s)
Loading gpm:all::init::population (epymorph.adrio.acs5.PopulationByAge):
  |####################| 100%  (0.000s)
Running simulation (BasicSimulator):
• 2020-01-01 to 2020-07-18 (200 days)
• 1 geo nodes
  |####################| 100% 
Runtime: 0.044s

• Use epymorph’s built-in feature to plot your model diagram (i.e., the box-and-arrow flow diagram of the system of equations).

rume.ipm.diagram()

• For the two possible events in the model (i.e., S->I, I->R), create a table that shows the total number events during the simulation.

out.table.sum(
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.events(),
)

	geo	quantity	sum
0	Mohave, AZ	S → I	12237
1	Mohave, AZ	I → R	12242

• For each of the compartments in the model, show the minimum, median, and maximum (i.e., quantiles) of the number of hosts that were present in each compartment throughout the simulation.

out.table.quantiles(
    quantiles=[0, 0.5, 1.0],
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.compartments(),
)

	geo	quantity	0	0.5	1.0
0	Mohave, AZ	S	6152.0	6154.0	18386.0
1	Mohave, AZ	I	0.0	9.0	1643.0
2	Mohave, AZ	R	0.0	12227.5	12242.0

Exercise 2

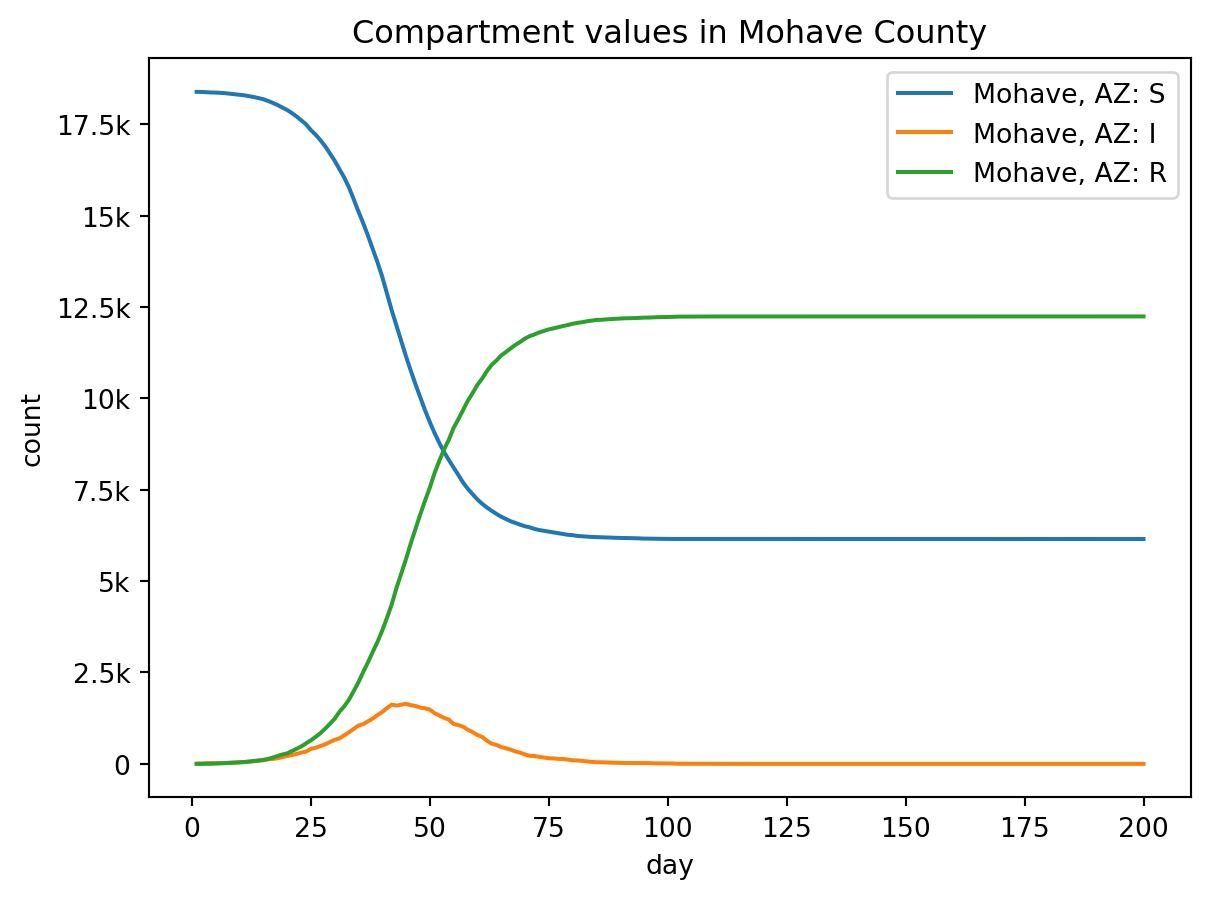
In textual terms, the output of a model is just a large array detailing the number of individuals in each model compartment over time, as well as the number of specific events that occur over time. To better represent these data, we usually want to view the model outputs graphically, i.e., as a graph of each compartment over time.

• Use the graphing functions available in epymorph to display the state variables over time on a graph embedded in your Jupyter notebook.

out.plot.line(
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.compartments(),
    title="Compartment values in Mohave County",
)

• Display the individual model events over time on a new graph.

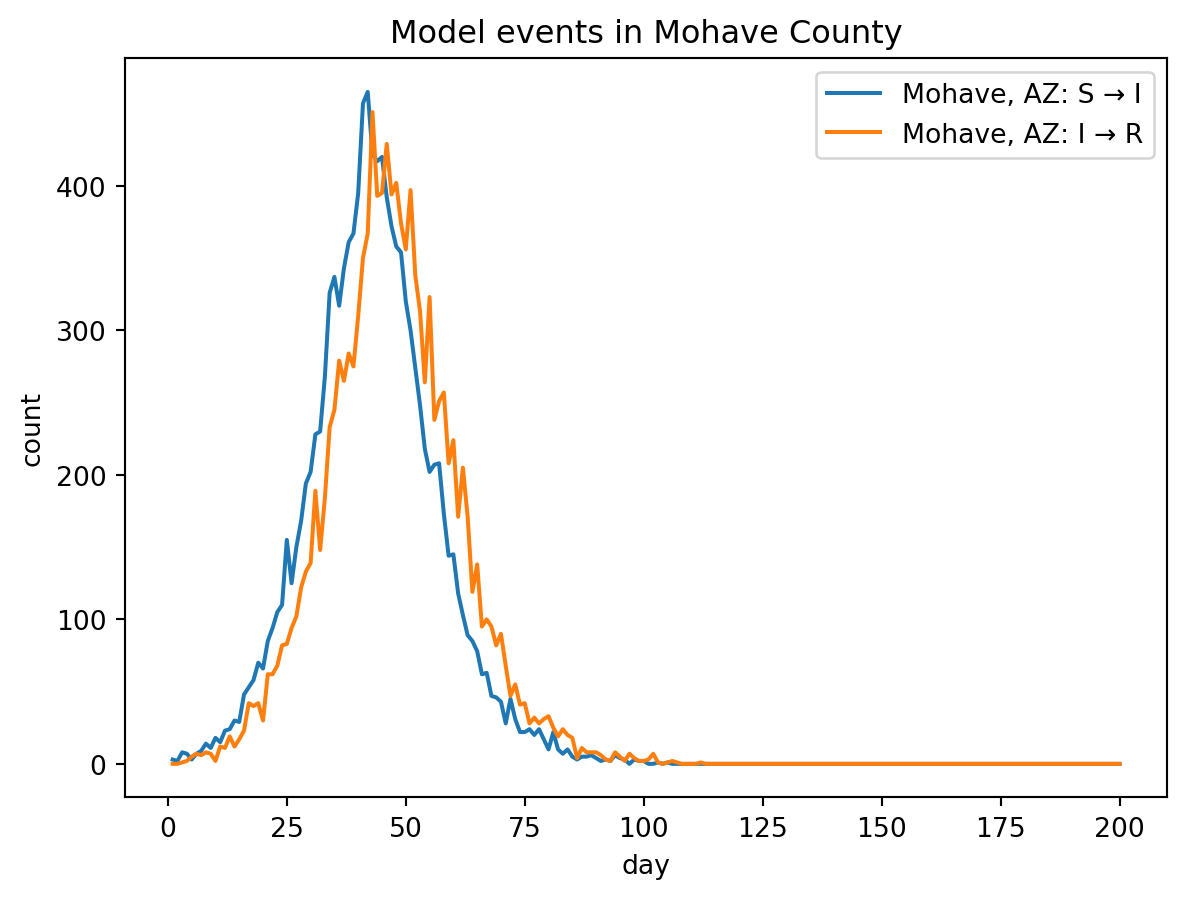
out.plot.line(
    geo=out.rume.scope.select.all(),
    time=out.rume.time_frame.select.all(),
    quantity=out.rume.ipm.select.events(),
    title="Model events in Mohave County",
)

Exercise 3

An important feature of all epymorph models is that they are stochastic, meaning that at each time step, a draw from a probability distribution determines which and how many transitions between model compartments (called “events”) occur. Thus, to get an accurate picture of the likely infections dynamics, one usually runs the model many times (called “realizations”); all of these runs are shown on the output graph, with the average of them highlighted and shown to show the most likely overall pattern.

• Now run a simulation for 20 realizations of the model

stored_sim_results = []
length = 20
for x in range(length):
    out = sim.run()
    stored_sim_results.append(out)

• Modify your plotting code to graph each realization as thin line

fig, ax = plt.subplots()

# This uses the more advanced line_plt() functionality
for j in stored_sim_results:
    j.plot.line_plt(
        ax = ax,
        geo=j.rume.scope.select.all(),
        time=j.rume.time_frame.select.all(),
        quantity=j.rume.ipm.select.events("S->I"),
    )

ax.set_xlabel("day")
ax.set_ylabel("S->I Events")
ax.set_title("Graph of 100 Simulation Results")
ax.grid(True)

fig.tight_layout()
plt.show()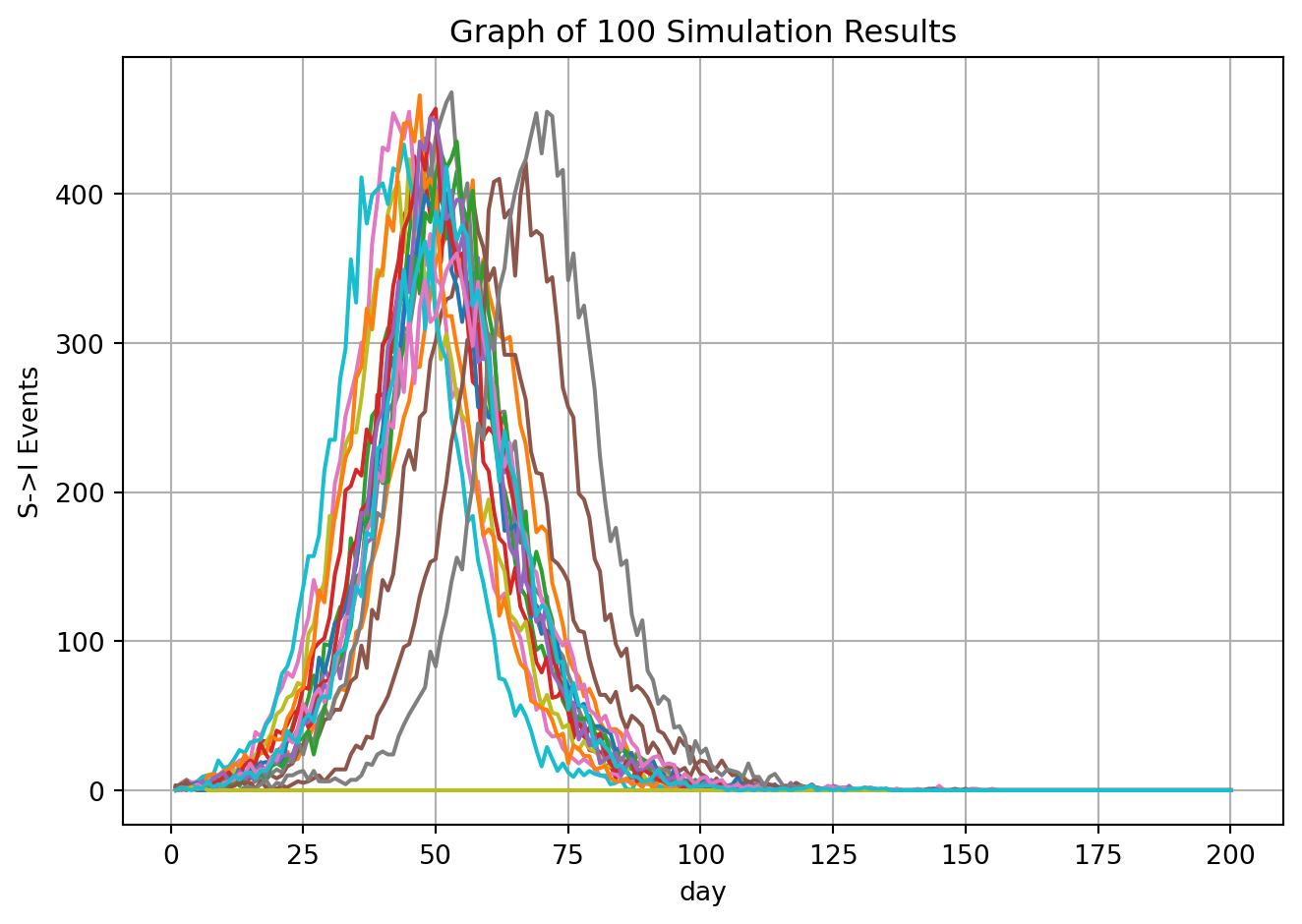

Exercise 4

ADVANCED Now that we have the basic model up and running, let’s use it to explore various disease dynamics in more detail.Because infected individuals are immune to measles after they recover, diseases like measles exhibit a disease “burnout”, where the infection rate drops to zero as the number of available susceptible individuals drops.

• Alter the transmission rate iteratively to show how the dynamics of the Infectious class over time changes.

beta_array = [0.33, 0.45, 0.8]
transmission_rates = []
for b in beta_array:
    rume = SingleStrataRUME.build(
        ipm=my_ipm,
        mm=null_mm,
        init=my_init,
        scope=scope,
        time_frame=time,
        params={
            "beta": b,
            "gamma": gam,
            "population": pop,
            "population_by_age_table": age,
        },
    )
    sim = BasicSimulator(rume)
    out = sim.run(
        rng_factory=default_rng(5),
    )

    transmission_rates.append(out)

• Specifically, create a plot to show how transmission rate affects the patterns of the Infectious class over time. This should show how the time to burnout depends on transmission rate.

fig, ax = plt.subplots()

for j in transmission_rates:
    j.plot.line_plt(
        ax = ax,
        geo=j.rume.scope.select.all(),
        time=j.rume.time_frame.select.all(),
        quantity=j.rume.ipm.select.compartments("I"),
    )

# custom graph
ax.set_xlabel("days")
ax.set_ylabel("Infected")
ax.set_title("Burnout")
ax.grid(True)

fig.tight_layout()
plt.show()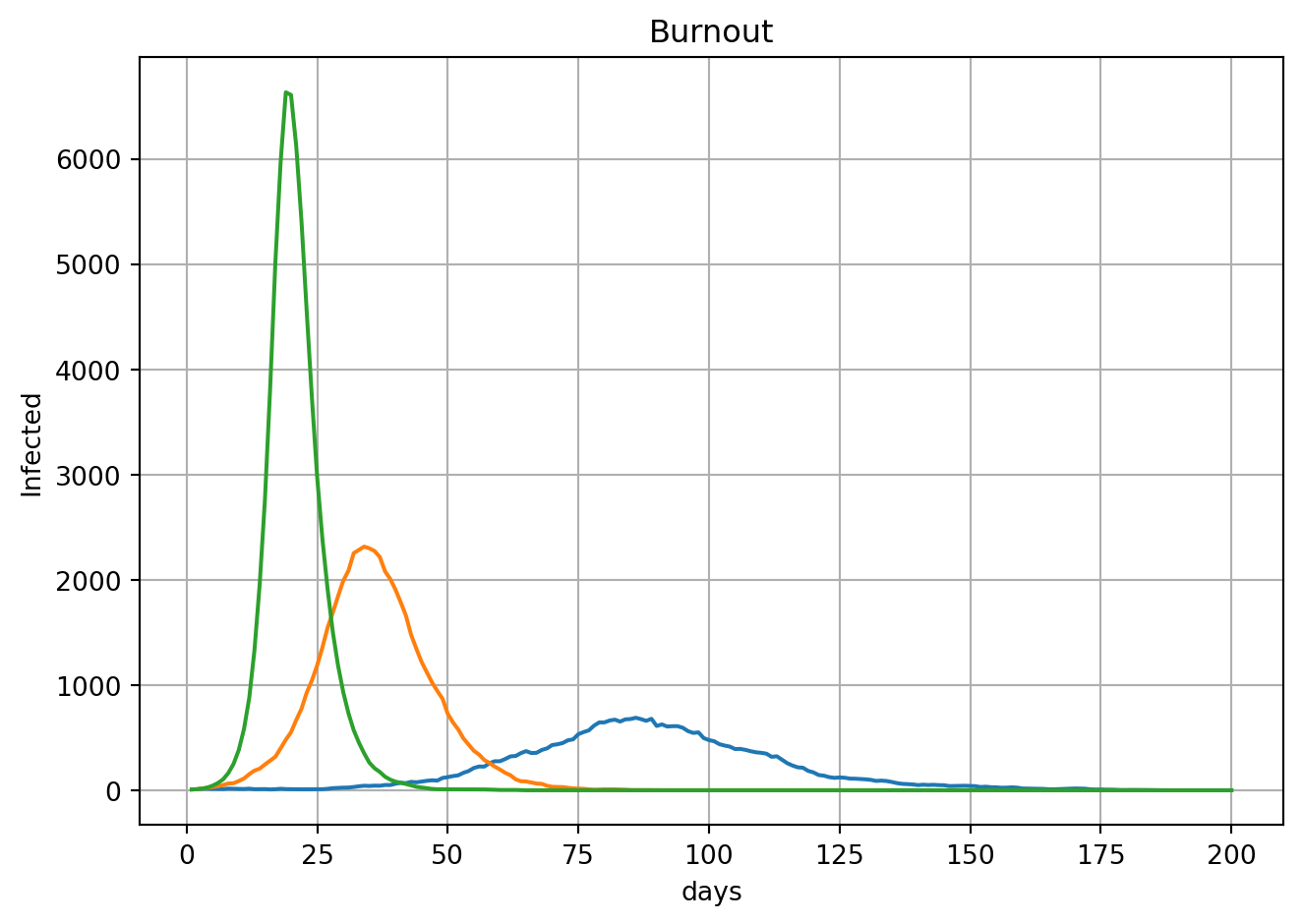

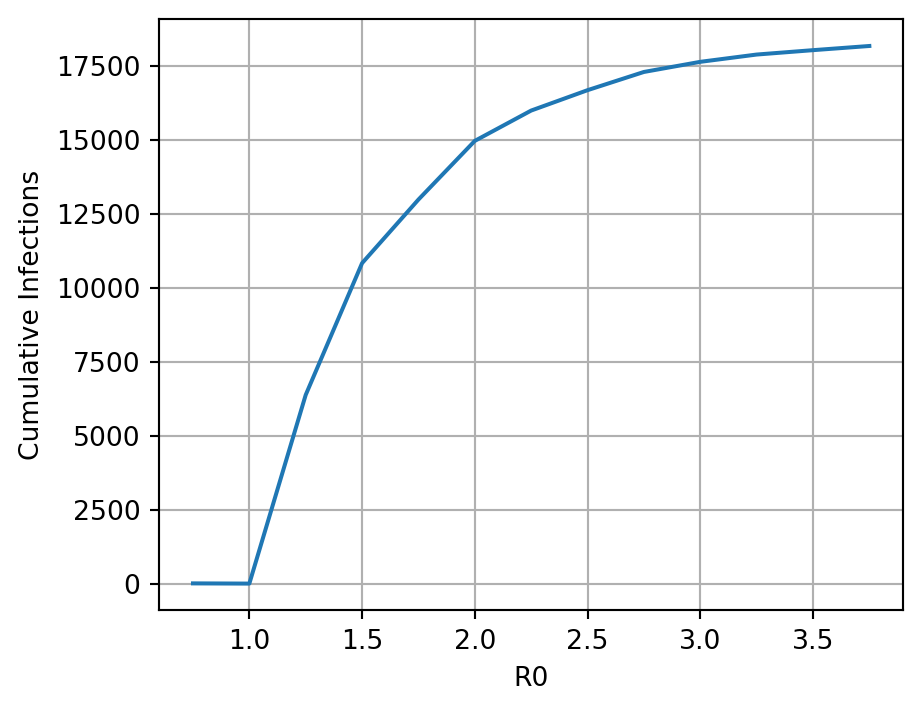
• The basic reproductive number of the pathogen (\(R0\)) in the SIR model is represented mathematically as the ratio of transmission rate to recovery rate: \(\beta / \gamma\). Iteratively alter the \(R0\) from ~0.01 to 10 and create a line plot to show how \(R0\) is associated with the total number of individuals that ultimately become infected during the outbreak. This number can be extracted as the number of Recovered individuals present at the last time step of the simulation, because remember that all Recovered individuals in this SIR model had been infected sometime in the past.

• Here the code is creating a simulation with different basic reproductive numbers of the pathogen for 6 different simulations and these R0 vals are being used to calculate a different beta val for each simulation. Total_outputs is storing the infections for each simulation.

total_outputs = []

R0_vals = np.arange(0.75, 4.0, 0.25)
beta_array = [x * gam for x in R0_vals]

for b in beta_array:
    rume = SingleStrataRUME.build(
        ipm=my_ipm,
        mm=null_mm,
        init=my_init,
        scope=scope,
        time_frame=time,
        params={
            "beta": b,
            "gamma": gam,
            "population": pop,
            "population_by_age_table": age,
        },
    )
    # run new sim here
    sim = BasicSimulator(rume)
    out = sim.run(
        rng_factory=default_rng(8),
    )

    # sum the I->R events over time to get cumulative
    current_output = out.table.sum(
        geo=rume.scope.select.all(),
        time=rume.time_frame.select.all(),
        quantity=rume.ipm.select.events("I->R"),
    )

    # Extract the sum column from the data frame
    total_outputs.append(current_output['sum'][0])

Now we plot the cumulative infections versus \(R0\). Note that the stochasticity will create a pattern that is close to the theoretical expectation, but not exactly.

plt.figure(figsize=(5, 4))
plt.plot(R0_vals, total_outputs)
plt.xlabel("R0")
plt.ylabel("Cumulative Infections")
plt.grid(True)
plt.show()